減衰振動
質量の無視できるバネの左端を固定し、右端に粒子mを結ぶ。
この粒子mが定点O(平衡位置)からxだけ変位した時、
これに、復元力: $-kx$の他に、その速度: $v = \dot{x}$に比例する抵抗$-b\dot{x}$
が働く場合、これに対する運動方程式は、次の様に与えられる。
\begin{align}
&F = m \ddot{x} = -kx -b\dot{x}\notag\\
&\leftrightarrow \begin{cases}
&\ddot{x} + 2\gamma\dot{x} + \omega_0^2x = 0\\
&\gamma \equiv \frac{b}{2m},\ \omega_0 \equiv \sqrt{\frac{k}{m}}
\end{cases}
\end{align}
一般解は、解$\lambda$によって、次の様に分類される。
- $\gamma = \omega_0$ (臨界減衰)、重根($\lambda = \lambda_1 = \lambda_2$)
\begin{align}
&x = e^{- \gamma t} (C_1+C_2t)
\end{align}
- $\gamma > \omega_0$ (過減衰)、相異なる実数根($\lambda_1,\lambda_2$)
\begin{align}
&x = C_1e^{\lambda_1 t} + C_2e^{\lambda_2 t}\notag\\
&\quad = e^{- \gamma t} [C_1e^{lt} + C_2e^{-lt}]
\end{align}
- $\gamma < \omega_0$ (減衰振動)、共役複素根($\lambda = - \gamma \pm il$)
\begin{align}
&x = C_1e^{\lambda_1 t} + C_2e^{\lambda_2 t}\notag\\
&\qquad \text{or}\notag\\
&x = e^{- \gamma t} [C_1\cos(lt) + C_2\sin(lt)]\notag\\
&\quad = A_0e^{-\gamma t} \cos(lt + \phi)
\end{align}
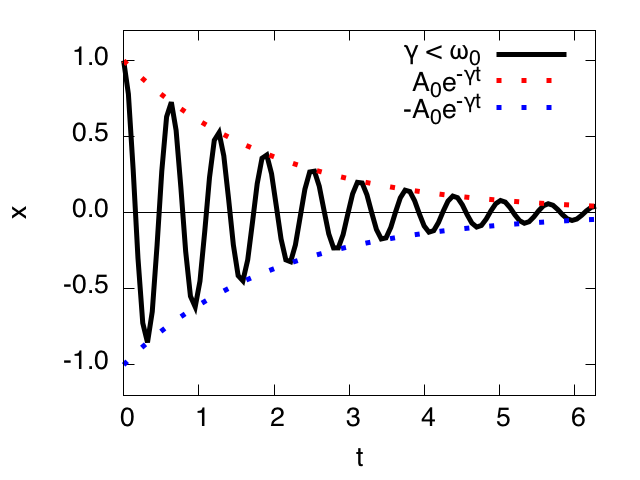
$\gamma < \omega_0$ (減衰振動): $A_0 = 1, \gamma = 0.5, l = 10, \phi = 0$。
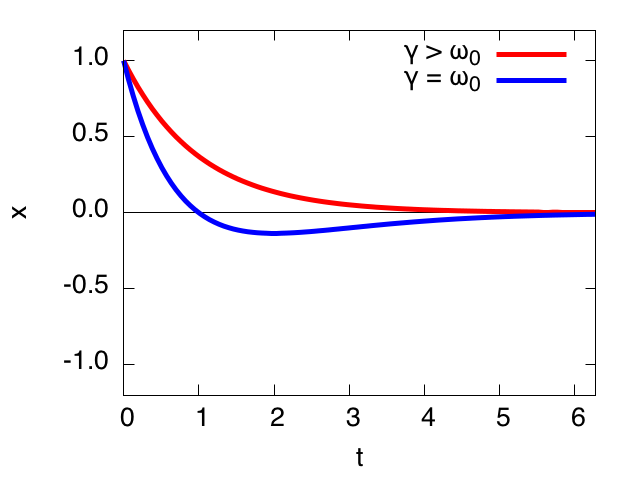
$\gamma > \omega_0$ (過減衰): $\gamma = 1, l = 0.1, C_1 = 0.5, C_2 = 0.5$。
$\gamma = \omega_0$ (臨界減衰): $\gamma = 1, C_11 = 1, C_22 = -1$。
強制振動(単振動 + 外力)
粒子mに復元力: $-kx$の他に、外部から角振動数$\omega$の周期的な力: $f\cos(\omega t)$が働く場合を考える。
この場合、粒子mに対する運動方程式は、次の様に与えられる。
\begin{align*}
&F = m\ddot{x} = -kx + f\cos(\omega t)\\
&\leftrightarrow \ddot{x} + \omega_0^2x = f_0 \cos(\omega t), \quad
\omega_0 \equiv \sqrt{\frac{k}{m}},\
f_0 \equiv \frac{f}{m}
\end{align*}
一般解は、
\begin{align*}
&x = [A\cos(\omega_0 t) + B\sin(\omega_0 t)] + \frac{f_0}{\omega_0^2 - \omega^2} \cos(\omega t)\\
&A = \frac{f_0}{\omega_0^2-\omega^2}
\end{align*}
となる。
このうち第1項は、この振動系が自主的に行う固有の振動を表し、これを$\bf{固有振動}$と呼ぶ。
これに対して、第2項は、外部からの周期的な力の作用によって振動系に引き起こされた振動を表し、これを$\bf{強制振動}$と呼ぶ。
強制振動(減衰振動 + 外力)
減衰振動に、外部から角振動数$\omega$の周期的な力: $f\cos(\omega t)$が働く場合について考える。
この場合、粒子mに対する運動方程式は、次の様な微分方程式になる。
\begin{align*}
&\ddot{x} + 2\gamma\dot{x} + \omega_0^2x = \frac{f}{m} \cos(\omega t), \quad \omega_0 > \gamma\\
&\leftrightarrow \ddot{x} + 2\gamma\dot{x} + \omega_0^2x = f_0 \cos(\omega t), \quad f_0 \equiv \frac{f}{m}
\end{align*}
一般解は、
\begin{align*}
&x = e^{- \gamma t} [C_1\cos(lt) + C_2\sin(lt)] + a \cos(\omega t - \phi)\notag\\
&\quad = A_0e^{-\gamma t} \cos(lt + \phi') + a \cos(\omega t - \phi)\\
&a = \frac{f_0}{\sqrt{(\omega_0^2-\omega^2)^2 + (2\gamma\omega)^2}}, \quad
\tan\phi = \frac{2\gamma\omega}{\omega_0^2 - \omega^2}
\end{align*}
となる。
ここで、$l \equiv \sqrt{\omega_0^2 - \gamma^2}$として用いた。
十分時間が経てば、この第1項の減衰振動は消えて、第2項の強制振動だけが残る。
振動の種類
これまで、学んだ振動の種類をまとめると、次の様に分類できる。
- 単振動
- 減衰振動
- 強制振動
- 強制振動(減衰振動 + 外力)
- 強制振動(単振動 + 外力)
\begin{align}
&\begin{cases}
&\bf{直角座標}\ (x,y,z)\\
&x = r \sin\theta \cos\phi\\
&y = r \sin\theta \sin\phi\\
&z = r \cos\theta
\end{cases}\\
&\leftrightarrow
\begin{cases}
&\bf{極座標}\ (r,\theta,\phi)\\
&r = \sqrt{x^2 + y^2 + z^2}\\
&\theta = \tan^{-1}(\sqrt{x^2 + y^2}/z)\\
&\phi = \tan^{-1}(y/x)
\end{cases}
\end{align}